D. Bigoni
Home
Research
Software
TransportMaps
DTU-UQ
DYTSI

Daniele Bigoni – Research

Topics of interest

  • Uncertainty quantification

  • Ordinary and partial differential equations

  • Numerical methods for differential equations

  • Machine learning

  • High-performance computing

  • Math and physics

Projects

  1. Measure transport for inference

  2. Uncertainty quantification with engineering applications

  3. Curving dynamics in high speed trains

Measure transport for inference (web-site)

We use (transport) maps to represent transformations between probability distributions. These transformations lead to efficient algorithms for the solution of practical inference problems, or for the estimation of densities from samples. Collaborators: Professor Youssef M. Marzouk, Alessio Spantini, Rebecca Morrison, Ricardo M. Baptista.

  1. [preprint] Bigoni, D., Zahm, O., Spantini, A., & Marzouk, Y. (2019). Greedy inference with layers of lazy maps, 1–15.

  2. [download, preprint] Spantini, A., Bigoni, D., & Marzouk, Y. (2018). Inference via low-dimensional couplings. Journal of Machine Learning Research, 19(66), 1–71.

  3. [ext.abstract] Bigoni, D., Spantini, A., & Marzouk, Y. (2016). Adaptive construction of measure transports for Bayesian inference.

  4. [ext.abstract] Spantini, A., Bigoni, D., & Marzouk, Y. (2016). Variational inference via decomposable transports : algorithms for Bayesian filtering and smoothing.

Scatter transform 

Uncertainty quantification with engineering applications (PhD - download)

I research both into novel techniques for uncertainty quantification and into applications of such techniques. In the following are listed some of the methodological and applied projects I'm involved in. The software for uncertainty quantification developed along the projects is collected in the DTU-UQ Library.
Supervisors: Associate Professor Allan P. Engsig-Karup, Professor Jan S. Hesthaven

  1. [download] Bigoni, D & Engsig-Karup, AP 2015, Uncertainty Quantification with Applications to Engineering Problems. Ph.D. thesis, Technical University of Denmark, Kgs. Lyngby. DTU Compute PHD-2014, no. 359

Spectral Tensor-Train Decomposition

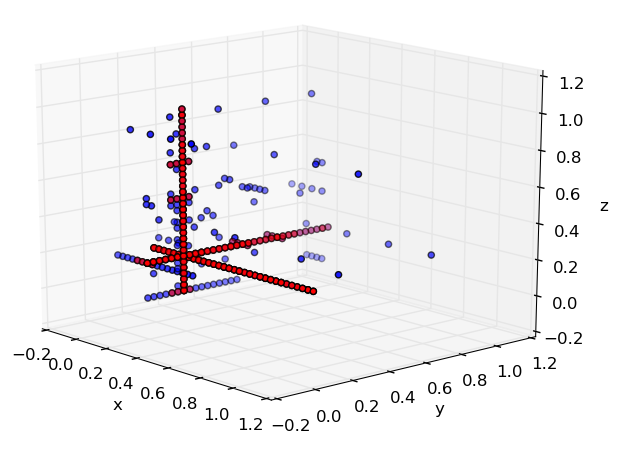QTTdmrg3d 

Extension of the tensor-train decomposition for the construction of approximations of complex and computationally expensive models. The aim is the construction of surrogates which point evaluation is an accurate representation of the full model and compuatationally inexpensive. The complex underlying model is given as a black box function and the surrogate must be constructed using an handful of function evaluations. The method promises to tackle and solve the curse of dimensionality, usually a bottleneck for novel techniques in uncertainty quantification.
In collaboration with:

  1. [preprint] Bigoni, D., Engsig-Karup, A. P., & Marzouk, Y. M. (2016). Spectral Tensor-Train Decomposition. SIAM Journal on Scientific Computing, 38(4), A2405–A2439. https://doi.org/10.1137/15M1036919

Sensitivity Analysis of the Critical Speed in Railway Vehicle Dynamics

Cut ANOVA Sensitivity analysis 

Study of the sensitivity of the Critical Speed of Railway Vehicles running on straight and curved tracks to the uncertainty on the suspension parameters. We present an approach to global sensitivity analysis aiming at the reduction of its computational cost without compromising the results. The method is based on sampling methods, cubature rules, Generalized Polynomial Chaos, High-Dimensional Model Representation and Total Sensitivity Indices. The numerical simulations of the vehicle dynamics have been performed using the program DYTSI.
In collaboration with:

  1. [postprint] Bigoni, D., Engsig-Karup, A. P., & True, H. (2012). Comparison of Classical and Modern Uncertainty Quantification Methods for the Calculation of Critical Speeds in Railway Vehicle Dynamics. In 13th mini Conference on Vehicle System Dynamics, Identification and Anomalies. Budapest, Hungary.

  2. [preprint] Bigoni, D., Engsig-Karup, A. P., & True, H. (2013). Modern Uncertainty Quantification Methods in Railroad Vehicle Dynamics. In ASME 2013 Rail Transportation Division Fall Technical Conference (p. V001T01A009). Altoona: ASME. doi:10.1115/RTDF2013-4713

  3. Bigoni, D., Engsig-Karup, A. P., & True, H. (2013). Anwendung der Uncertainty Quantification bei eisenbahndynamischen problemen. Z E Vrail - Glasers Annalen, 137(SPL.ISSUE), 152–158.

  4. [preprint] Bigoni, D., True, H., & Engsig-Karup, A. P. (2013). Sensitivity Analysis of the critical speed in railway vehicle dynamics. In 23rd IAVSD Symposium on Dynamics of Vehicles on Roads and Tracks (pp. 1–9). Qingdao.

  5. [preprint] Bigoni, D., True, H., & Engsig-Karup, A. P. (2014). Sensitivity analysis of the critical speed in railway vehicle dynamics. Vehicle System Dynamics, (May 2014), 272–286. doi:10.1080/00423114.2014.898776

  6. [preprint] Bigoni, D., Engisg-Karup, A. P., & True, H. (2014). Global Sensitivity Analysis of Railway Vehicle Dynamics on Curved Tracks. In Volume 2: Dynamics, Vibration and Control; Energy; Fluids Engineering; Micro and Nano Manufacturing (p. V002T07A023). Copenhagen, Denmark: ASME. doi:10.1115/ESDA2014-20529

Uncertainty quantification on free surface water wave simulation

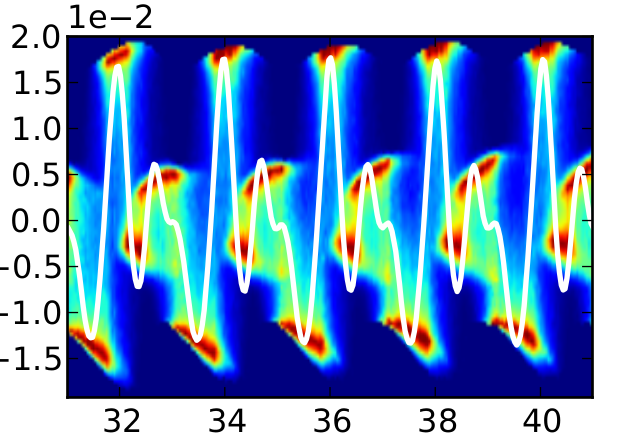UQ Water Waves 

Study of free surface water waves subject to uncertain wave properties and bathymetry. The aim is to combine state of the art software for the simulation of free surface water waves with efficient techniques for uncertainty quantification. The highly efficient GPU-accelerated library OceanWave3D is used to solve the many realizations needed in order to study the uncertainty. The dymensionality of the stochastic system is reduced with techniques for model reduction, while the uncertainty is studied with deterministic collocation methods.
In collaboration with:

  1. [preprint] Bigoni, D., Engsig-Karup, A. P., & Eskilsson, C. (2016). Efficient uncertainty quantification of a fully nonlinear and dispersive water wave model with random inputs. Journal of Engineering Mathematics, 101(1), 87–113. https://doi.org/10.1007/s10665-016-9848-8

  2. [preprint] Engsig-Karup, A. P., Eskilsson, C., & Bigoni, D. (2016). A stabilised nodal spectral element method for fully nonlinear water waves. Journal of Computational Physics, 318, 1–21. article. https://doi.org/10.1016/j.jcp.2016.04.060

Curving Dynamics in High Speed Trains (Master Thesis - download)

TGV 

Modeling and implementation of a railway vehicle running on straight or curved track with different profiles. The model employs the Newton-Euler formulation for dynamical systems. The wheel-rail interaction is modeled using the Hertz's static contact theory, corrected with the Kalker's theory for dynamical wheel-rail penetration, and Shen, Hedrick and Elkins non-linear theory. The model is implemented in the program DYTSI. This is a framework for designing and testing railway vehicle models and it includes a number of numerical ODE solvers. The hunting phenomenon has been studied on the Cooperrider model on straight and curved track. Additional results have been obtained for a complete wagon model and the symmetry assumption of the model running on straight track was rejected as different behaviors for the leading and trailing parts were obtained. On curved tracks the passage from the subcritical Hopf bifurcation to the super critical Hopf bifurcation was confirmed, for certain radii, also for the complete wagon model.
The dynamics of an AGV model, provided by ALSTOM, have been studied on curves with big radii and high cant deficiency. The results obtained, for the model running on smooth tracks, have been confirmed.

Under the supervision of:

  1. [download] Bigoni, D. (2011). Curving Dynamics in High Speed Trains. Master Thesis.

  2. [preprint] True, H., Engsig-Karup, A. P., & Bigoni, D. (2014). On the numerical and computational aspects of non-smoothnesses that occur in railway vehicle dynamics. Mathematics and Computers in Simulation, 95, 78–97. doi:10.1016/j.matcom.2012.09.016